Materi Matematika Fungsi dan Relasi

Berita Terkait

Materi matematika fungsi dan relasi merupakan konsep dasar yang penting dalam matematika. Konsep ini menjelaskan hubungan antara dua variabel atau lebih, dan memiliki berbagai penerapan dalam kehidupan sehari-hari, serta dalam berbagai bidang studi lainnya. Dari definisi sederhana hingga operasi kompleks, materi ini akan membahas berbagai aspek penting fungsi dan relasi, sehingga memudahkan pemahaman.

Materi ini akan menguraikan definisi fungsi dan relasi, jenis-jenis fungsi, konsep relasi, operasi pada fungsi, grafik fungsi dan relasi, serta penerapannya dalam matematika dan kehidupan nyata. Dengan pemahaman yang baik, diharapkan pembaca mampu memahami dan menerapkan konsep fungsi dan relasi dengan mudah.

Definisi Materi Fungsi dan Relasi

Fungsi dan relasi merupakan konsep dasar dalam matematika yang menjelaskan hubungan antara dua himpunan. Pemahaman tentang fungsi dan relasi sangat penting dalam berbagai bidang studi, mulai dari ilmu alam hingga ilmu sosial.

Definisi Fungsi dan Relasi

Relasi adalah hubungan antara anggota himpunan yang satu dengan anggota himpunan yang lain. Fungsi adalah suatu relasi khusus di mana setiap anggota himpunan pertama (domain) dipasangkan tepat dengan satu anggota himpunan kedua (kodomain). Perbedaan mendasarnya terletak pada keunikan pasangan. Relasi dapat memiliki beberapa pasangan untuk anggota himpunan pertama, sementara fungsi hanya memiliki satu pasangan untuk setiap anggota himpunan pertama.

Perbedaan Fungsi dan Relasi

Aspek	Relasi	Fungsi
Hubungan	Hubungan antara anggota himpunan A dan B	Hubungan khusus di mana setiap anggota himpunan A dipasangkan tepat dengan satu anggota himpunan B
Keunikan Pasangan	Satu anggota himpunan A dapat dipasangkan dengan beberapa anggota himpunan B	Satu anggota himpunan A dipasangkan tepat dengan satu anggota himpunan B
Contoh	Setiap siswa dengan nilai ujiannya	Setiap siswa dengan nilai ujiannya (dengan catatan setiap siswa hanya mendapatkan satu nilai)

Contoh Fungsi dan Relasi dalam Kehidupan Sehari-hari

Penerapan fungsi dan relasi dalam kehidupan sehari-hari sangatlah banyak. Misalnya, setiap orang memiliki nomor KTP yang unik. Hal ini merupakan contoh fungsi karena setiap orang dihubungkan dengan satu nomor KTP, tidak ada yang memiliki dua nomor KTP yang berbeda. Contoh relasi adalah hubungan antara waktu dan suhu. Pada suatu hari, suhu dapat berubah-ubah sepanjang hari, dan waktu tertentu dapat berhubungan dengan suhu tertentu.

Harga barang dan kuantitas: Setiap kuantitas barang memiliki harga tertentu. Ini merupakan fungsi, karena satu kuantitas barang hanya memiliki satu harga. Jika ada dua harga untuk kuantitas yang sama, maka ini bukan fungsi.
Nilai tukar mata uang: Nilai tukar mata uang terhadap mata uang lain merupakan fungsi. Satu mata uang akan memiliki nilai tukar tertentu terhadap mata uang lainnya.
Tarif parkir: Tarif parkir berdasarkan lama parkir merupakan fungsi. Waktu parkir tertentu dihubungkan dengan tarif parkir tertentu. Ini merupakan contoh sederhana dari konsep fungsi dalam kehidupan sehari-hari.

Penerapan Fungsi dan Relasi di Berbagai Bidang Studi

Konsep fungsi dan relasi memiliki aplikasi luas dalam berbagai bidang studi. Dalam ilmu fisika, misalnya, fungsi digunakan untuk memodelkan hubungan antara variabel-variabel fisik. Dalam ilmu ekonomi, fungsi permintaan dan penawaran digunakan untuk menganalisis pasar. Dalam ilmu komputer, fungsi digunakan untuk melakukan operasi-operasi tertentu pada data.

Ilmu Komputer: Fungsi digunakan untuk memodelkan algoritma dan prosedur. Setiap input akan dipetakan ke output tunggal, mengikuti aturan tertentu.
Ilmu Ekonomi: Fungsi permintaan dan penawaran digunakan untuk menganalisis bagaimana harga dan kuantitas barang atau jasa berinteraksi.
Ilmu Alam: Fungsi digunakan untuk memodelkan hubungan antara besaran-besaran fisik, seperti kecepatan dan waktu, atau gaya dan percepatan.

Jenis-Jenis Fungsi

Pemahaman tentang berbagai jenis fungsi matematika sangat penting dalam berbagai bidang, mulai dari ilmu alam hingga ekonomi. Masing-masing jenis fungsi memiliki karakteristik dan penerapan yang unik.

Fungsi Linear

Fungsi linear merupakan fungsi yang paling sederhana. Grafiknya berupa garis lurus. Persamaan umumnya berbentuk f(x) = mx + c, di mana m adalah gradien dan c adalah titik potong sumbu-y. Domain dan range fungsi linear adalah semua bilangan real.

Persamaan: f(x) = mx + c
Grafik: Garis lurus
Domain: Semua bilangan real
Range: Semua bilangan real
Contoh Penerapan: Menghitung biaya taksi berdasarkan jarak tempuh, menghitung total harga barang dengan harga satuan tetap.

Fungsi Kuadrat

Fungsi kuadrat memiliki grafik berupa parabola. Persamaan umumnya berbentuk f(x) = ax² + bx + c, di mana a, b, dan c adalah konstanta. Domain fungsi kuadrat adalah semua bilangan real. Range-nya bergantung pada nilai a dan dapat berupa interval tertentu.

Persamaan: f(x) = ax² + bx + c
Grafik: Parabola
Domain: Semua bilangan real
Range: Bergantung pada nilai a, bisa berupa interval tertentu
Contoh Penerapan: Menentukan tinggi benda yang dilempar ke atas, menghitung luas persegi panjang dengan sisi yang berubah.

Fungsi Polinomial

Fungsi polinomial merupakan perluasan dari fungsi kuadrat. Grafiknya bisa berupa kurva yang kompleks, tergantung pada derajat polinomial. Domain fungsi polinomial adalah semua bilangan real. Range-nya bisa berupa interval tertentu atau semua bilangan real.

Persamaan: Umumnya berbentuk f(x) = a_nx ⁿ + a _n-1x ^n-1 + … + a ₁x + a ₀
Grafik: Kurva yang kompleks, tergantung pada derajat polinomial
Domain: Semua bilangan real
Range: Bergantung pada derajat dan koefisien polinomial
Contoh Penerapan: Memprediksi pertumbuhan populasi, memodelkan perilaku suatu sistem fisik.

Fungsi Rasional

Fungsi rasional adalah hasil bagi dua fungsi polinomial. Grafiknya dapat memiliki asimtot (garis yang didekati oleh grafik tetapi tidak pernah disentuh). Domainnya adalah semua bilangan real kecuali nilai-nilai yang membuat penyebut sama dengan nol. Range-nya dapat berupa interval tertentu atau semua bilangan real.

Persamaan: f(x) = p(x)/q(x), dengan p(x) dan q(x) adalah polinomial
Grafik: Dapat memiliki asimtot
Domain: Semua bilangan real kecuali nilai-nilai yang membuat q(x) = 0
Range: Bergantung pada persamaan fungsi
Contoh Penerapan: Menghitung kepadatan penduduk, menghitung kecepatan rata-rata.

Fungsi Eksponensial

Fungsi eksponensial memiliki variabel sebagai eksponen. Grafiknya meningkat atau menurun secara eksponensial. Domainnya adalah semua bilangan real. Range-nya adalah semua bilangan positif.

Persamaan: f(x) = a^x, dengan a > 0 dan a ≠ 1
Grafik: Mmeningkat atau menurun secara eksponensial
Domain: Semua bilangan real
Range: Semua bilangan real positif
Contoh Penerapan: Pertumbuhan bakteri, peluruhan radioaktif.

Fungsi Logaritma, Materi matematika fungsi dan relasi

Fungsi logaritma adalah kebalikan dari fungsi eksponensial. Grafiknya meningkat atau menurun. Domainnya adalah semua bilangan real positif. Range-nya adalah semua bilangan real.

Persamaan: f(x) = log_a(x) , dengan a > 0 dan a ≠ 1
Grafik: Meningkat atau menurun
Domain: Semua bilangan real positif
Range: Semua bilangan real
Contoh Penerapan: Menentukan magnitudo gempa bumi, menghitung tingkat kebisingan.

Konsep Relasi

Relasi merupakan hubungan antara dua himpunan. Konsep ini menjadi dasar dalam memahami berbagai konsep matematika, termasuk fungsi. Memahami relasi dan karakteristiknya akan mempermudah pemahaman konsep-konsep selanjutnya.

Penjelasan Dasar Relasi

Relasi antara dua himpunan, A dan B, dapat didefinisikan sebagai hubungan yang menghubungkan setiap elemen di himpunan A dengan satu atau lebih elemen di himpunan B. Himpunan A disebut domain dan himpunan B disebut kodomain. Range adalah himpunan bagian dari kodomain yang berisi semua elemen yang memiliki pasangan di domain.

Contoh Relasi yang Bukan Fungsi

Berikut adalah contoh relasi yang bukan fungsi:

Misalkan himpunan A = 1, 2, 3 dan himpunan B = 4, 5, 6. Relasi yang menghubungkan setiap elemen di A dengan dua elemen di B bukanlah fungsi. Sebagai contoh, jika 1 dihubungkan dengan 4 dan 5, 2 dihubungkan dengan 5 dan 6, dan 3 dihubungkan dengan 6 dan 4. Ini bukan fungsi karena elemen di A memiliki lebih dari satu pasangan di B.
Relasi yang memasangkan setiap mahasiswa dengan semua mata kuliah yang diambilnya. Setiap mahasiswa bisa mengambil banyak mata kuliah, sehingga bukan fungsi karena satu input (mahasiswa) bisa memetakan ke banyak output (mata kuliah).

Hubungan Antara Domain, Kodomain, dan Range

Untuk memahami hubungan antara domain, kodomain, dan range, berikut contoh tabelnya:

Relasi	Domain	Kodomain	Range
Relasi antara siswa dengan nilai ujian	Andi, Budi, Citra	80, 90, 75, 85, 95	80, 90, 75, 85
Relasi antara bilangan dengan kuadratnya	1, 2, 3	1, 4, 9, 16	1, 4, 9

Menentukan Relasi Sebagai Fungsi

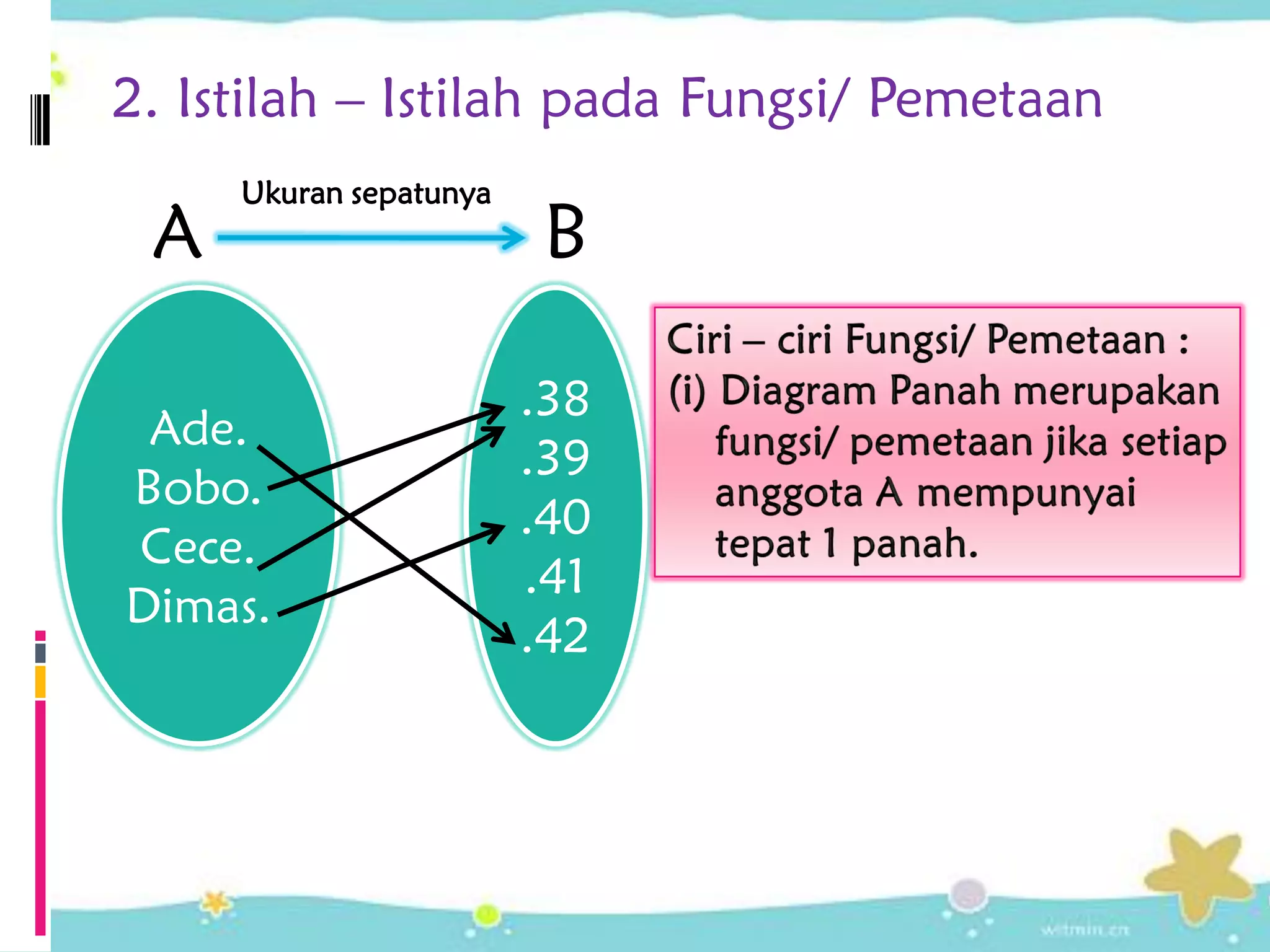
Suatu relasi dapat dianggap sebagai fungsi jika setiap elemen di domain hanya memiliki satu pasangan di kodomain. Jika ada elemen di domain yang memiliki lebih dari satu pasangan di kodomain, maka relasi tersebut bukanlah fungsi.

Menyatakan Relasi

Relasi dapat dinyatakan dalam beberapa cara, antara lain:

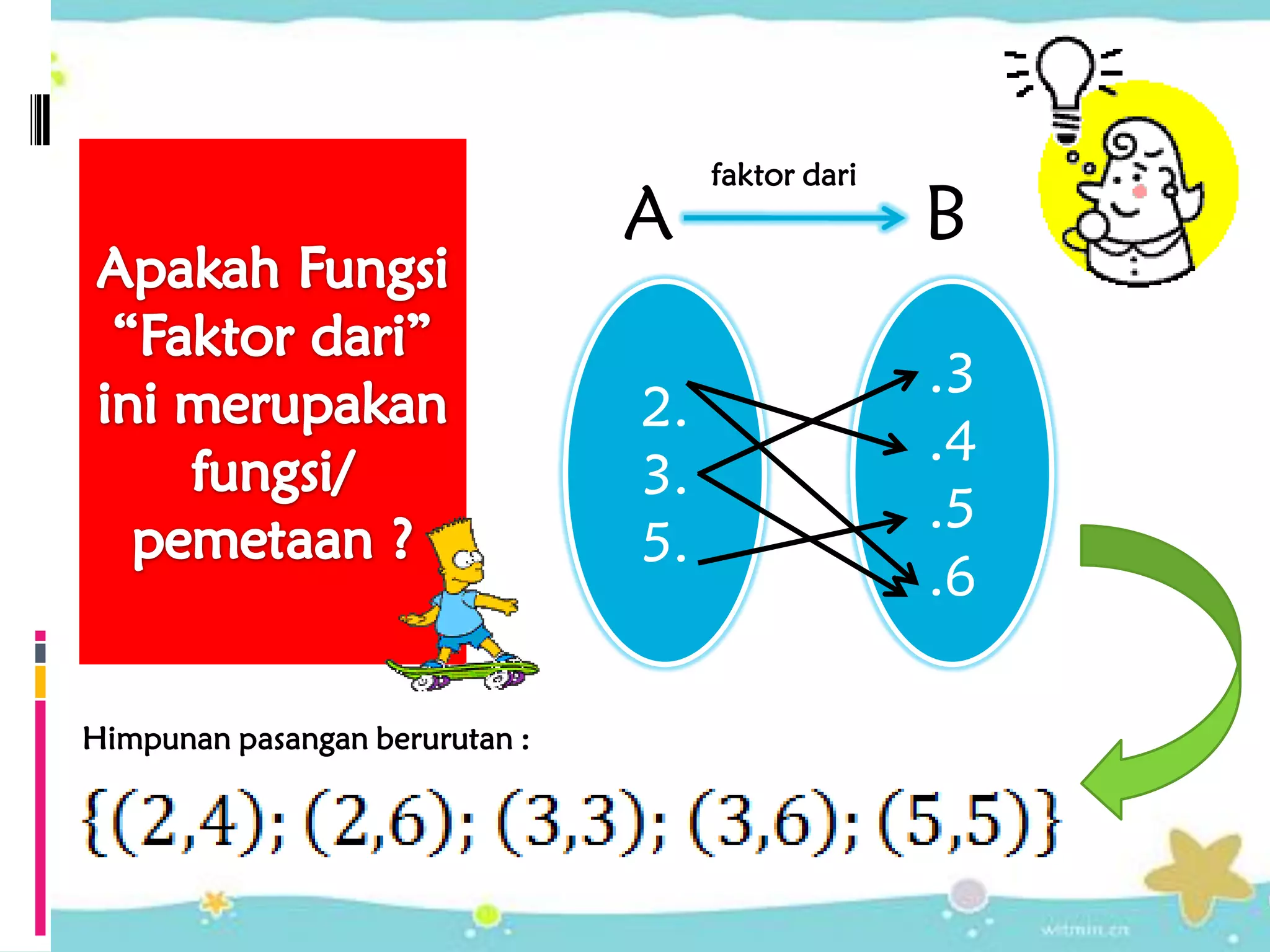
Diagram Panah: Diagram panah memperlihatkan hubungan antar elemen domain dan kodomain dengan anak panah.
Himpunan Pasangan Berurutan: Himpunan pasangan berurutan mencatat setiap pasangan terurut (elemen domain, elemen kodomain) yang terhubung oleh relasi.

Misalnya, relasi (1, 4), (2, 5), (3, 6) menunjukkan bahwa 1 dihubungkan dengan 4, 2 dihubungkan dengan 5, dan 3 dihubungkan dengan 6. Ini merupakan contoh sederhana relasi yang dapat dinyatakan dengan diagram panah.

Operasi pada Fungsi

Memahami operasi pada fungsi sangat penting dalam matematika. Operasi ini memungkinkan kita untuk menggabungkan dan memanipulasi fungsi-fungsi untuk mendapatkan fungsi baru. Dengan pemahaman yang baik, kita dapat menganalisis dan memecahkan berbagai permasalahan yang melibatkan fungsi.

Penjumlahan dan Pengurangan Fungsi

Penjumlahan dan pengurangan fungsi dilakukan dengan menjumlahkan atau mengurangkan nilai fungsi pada setiap titik. Misalnya, jika diberikan fungsi f(x) dan g(x), maka:

(f + g)(x) = f(x) + g(x)
(f – g)(x) = f(x)
-g(x)

Contoh:

Misalkan f(x) = 2x + 1 dan g(x) = x²
-3 . Maka:

(f + g)(x) = (2x + 1) + (x ²
-3) = x ² + 2x – 2
(f – g)(x) = (2x + 1)
-(x ²
-3) = -x ² + 2x + 4

Perkalian dan Pembagian Fungsi

Perkalian dan pembagian fungsi dilakukan dengan mengalikan atau membagi nilai fungsi pada setiap titik. Perlu diingat bahwa pembagian fungsi hanya didefinisikan jika penyebutnya tidak nol.

(f ⋅ g)(x) = f(x) ⋅ g(x)
(f / g)(x) = f(x) / g(x), dengan syarat g(x) ≠ 0

Contoh:

Jika f(x) = x dan g(x) = x + 2, maka:

(f ⋅ g)(x) = x(x + 2) = x ² + 2x
(f / g)(x) = x / (x + 2), dengan syarat x ≠ -2

Komposisi Fungsi

Komposisi fungsi adalah penerapan satu fungsi pada hasil dari fungsi lainnya. Jika kita memiliki fungsi f(x) dan g(x), maka komposisi fungsi f dikomposisikan dengan g dinotasikan sebagai ( f o g)( x) atau f( g( x)).

(f o g)(x) = f(g(x))

Contoh:

Misalkan f(x) = x² dan g(x) = x + 1. Maka:

(f o g)(x) = f(g(x)) = f(x + 1) = (x + 1) ² = x ² + 2x + 1

Tabel Rumus Operasi Fungsi

Operasi	Rumus
Penjumlahan	(f + g)(x) = f(x) + g(x)
Pengurangan	(f – g)(x) = f(x) g(x)
Perkalian	(f ⋅ g)(x) = f(x) ⋅ g(x)
Pembagian	(f / g)(x) = f(x) / g(x), g(x) ≠ 0
Komposisi	(f o g)(x) = f(g(x))

Grafik Fungsi dan Relasi

Grafik fungsi dan relasi merupakan representasi visual dari hubungan antara variabel. Dengan melihat grafik, kita dapat memahami pola dan karakteristik hubungan tersebut dengan lebih mudah.

Penggambaran Hubungan Antar Variabel

Grafik berfungsi sebagai alat visualisasi yang efektif untuk memahami bagaimana variabel-variabel terkait satu sama lain. Melalui grafik, kita dapat melihat tren, pola, dan perilaku hubungan tersebut, sehingga analisis data menjadi lebih mudah dan informatif. Grafik dapat menunjukkan apakah hubungannya linier, kuadratik, eksponensial, atau jenis hubungan lainnya. Informasi ini sangat berharga dalam berbagai aplikasi, mulai dari ilmu pengetahuan hingga bisnis.

Contoh Grafik Fungsi dan Relasi

Berikut beberapa contoh grafik fungsi dan relasi yang berbeda:

Fungsi linier: Grafiknya berupa garis lurus. Contoh: y = 2x + 1
Fungsi kuadratik: Grafiknya berupa parabola. Contoh: y = x²
-3x + 2
Fungsi eksponensial: Grafiknya meningkat atau menurun secara eksponensial. Contoh: y = 2 ^x
Relasi yang bukan fungsi: Grafiknya dapat berupa kurva yang tidak memenuhi uji garis vertikal. Contoh: x = y²

Jenis-Jenis Grafik Fungsi dan Relasi

Berikut tabel yang merangkum beberapa jenis grafik fungsi dan relasi beserta karakteristiknya:

Jenis Grafik	Bentuk Grafik	Contoh Persamaan
Fungsi Linier	Garis Lurus	y = mx + c
Fungsi Kuadratik	Parabola	y = ax² + bx + c
Fungsi Eksponensial	Kurva Naik/Turun Eksponensial	y = a^x
Fungsi Rasional	Kurva dengan asimtot	y = p(x)/q(x)
Fungsi Trigonometri	Berkaitan dengan sudut dan perbandingan sisi segitiga	y = sin(x), y = cos(x), y = tan(x)

Menentukan Persamaan Fungsi dari Grafik

Persamaan fungsi dapat ditentukan dari grafik dengan mengidentifikasi titik-titik penting pada grafik, seperti titik potong sumbu, kemiringan garis, atau puncak parabola. Kemudian, substitusikan titik-titik tersebut ke dalam bentuk umum persamaan fungsi yang sesuai untuk menentukan nilai konstanta.

Fungsi linier: Tentukan dua titik pada grafik dan hitung gradien (kemiringan). Gunakan rumus persamaan garis lurus (y = mx + c) untuk menentukan persamaan.
Fungsi kuadratik: Tentukan titik puncak dan satu titik lain pada grafik. Substitusikan ke dalam bentuk umum persamaan fungsi kuadratik (y = ax² + bx + c) untuk mendapatkan nilai konstanta.

Menggambar Grafik Fungsi dan Relasi dari Persamaannya

Menggambar grafik fungsi atau relasi dari persamaannya melibatkan beberapa langkah:

Tentukan titik-titik penting: Tentukan titik potong sumbu x dan y, titik ekstrem (puncak/minimum), dan asimtot (jika ada).
Buat tabel nilai: Buat tabel yang berisi nilai-nilai x dan y yang sesuai dengan persamaan.
Plot titik-titik pada koordinat kartesius: Plot titik-titik yang telah dihitung pada bidang koordinat.
Hubungkan titik-titik: Hubungkan titik-titik tersebut untuk mendapatkan grafik fungsi atau relasi.

Penerapan Fungsi dan Relasi dalam Matematika

Fungsi dan relasi bukanlah sekadar konsep abstrak dalam matematika. Konsep-konsep ini memiliki beragam penerapan praktis dalam kehidupan sehari-hari dan berbagai disiplin ilmu. Memahami penerapannya akan memperkaya pemahaman kita tentang bagaimana matematika berperan dalam menyelesaikan masalah dan memodelkan fenomena.

Penerapan dalam Pemecahan Masalah Matematika

Fungsi dan relasi berperan penting dalam memecahkan berbagai masalah matematika. Misalnya, dalam menentukan hubungan antara variabel dalam suatu persamaan, atau memodelkan pola pertumbuhan suatu barisan. Dengan menggunakan fungsi, kita dapat menganalisis hubungan sebab-akibat dan memprediksi hasil.

Dalam menyelesaikan persamaan linier, kita menggunakan fungsi linear untuk menemukan solusi.
Dalam analisis data, fungsi dapat digunakan untuk menggambarkan tren dan pola.
Dalam geometri, relasi digunakan untuk menjelaskan hubungan antara titik-titik dan bangun-bangun.

Penerapan di Bidang Studi Lain

Fungsi dan relasi bukan hanya bermanfaat dalam matematika, tetapi juga dalam disiplin ilmu lainnya. Misalnya, dalam fisika, fungsi digunakan untuk menggambarkan hubungan antara gaya dan percepatan, atau antara energi dan waktu. Dalam kimia, fungsi digunakan untuk menggambarkan hubungan antara konsentrasi zat dan laju reaksi. Di bidang ekonomi, fungsi digunakan untuk memodelkan hubungan antara permintaan dan penawaran, atau untuk memprediksi pertumbuhan ekonomi.

Fisika: Fungsi digunakan untuk merepresentasikan hubungan antara variabel fisika, seperti gaya dan percepatan, atau energi dan waktu. Contohnya, hukum Newton tentang gerak menggambarkan hubungan antara gaya yang bekerja pada benda dengan percepatan yang dihasilkan.
Kimia: Fungsi dapat digunakan untuk memodelkan laju reaksi kimia, hubungan antara konsentrasi zat dan kesetimbangan reaksi. Contohnya, persamaan laju reaksi menggambarkan bagaimana laju reaksi bergantung pada konsentrasi reaktan.
Ekonomi: Fungsi permintaan dan penawaran digunakan untuk menganalisis pasar dan memprediksi harga. Fungsi produksi digunakan untuk memodelkan hubungan antara input produksi (buruh, modal) dan output (produksi). Contohnya, fungsi produksi dapat digunakan untuk menentukan berapa banyak output yang dapat dihasilkan dengan jumlah input tertentu.

Ilustrasi Penerapan dalam Dunia Nyata

Pertumbuhan penduduk dapat diilustrasikan dengan fungsi eksponensial. Grafik pertumbuhan penduduk akan menunjukkan bagaimana jumlah penduduk meningkat seiring berjalannya waktu. Model ini membantu dalam perencanaan pembangunan dan memprediksi kebutuhan di masa depan.

Ilustrasi lain adalah dalam bidang keuangan. Fungsi dapat digunakan untuk menghitung bunga, atau menghitung nilai investasi pada jangka waktu tertentu.

Langkah-Langkah Menyelesaikan Soal Fungsi dan Relasi

Berikut langkah-langkah umum dalam menyelesaikan soal yang melibatkan fungsi dan relasi:

Identifikasi variabel-variabel yang terlibat dan hubungan di antara mereka.
Tentukan jenis fungsi atau relasi yang sesuai untuk memodelkan hubungan tersebut.
Jika perlu, tentukan nilai-nilai variabel yang diketahui.
Substitusikan nilai-nilai yang diketahui ke dalam fungsi atau relasi.
Selesaikan persamaan atau pertidaksamaan yang dihasilkan untuk mendapatkan nilai yang dicari.

Memodekan Fenomena Kehidupan Sehari-hari

Konsep fungsi dan relasi memungkinkan kita untuk memodelkan berbagai fenomena dalam kehidupan sehari-hari. Misalnya, kita dapat memodelkan hubungan antara waktu dan jarak yang ditempuh oleh suatu benda yang bergerak dengan kecepatan konstan. Kita juga dapat memodelkan hubungan antara suhu dan volume suatu zat. Dengan memodelkan fenomena tersebut, kita dapat memprediksi dan memahami bagaimana hal-hal tersebut terjadi.

Contoh Soal dan Latihan: Materi Matematika Fungsi Dan Relasi

Berikut disajikan beberapa contoh soal dan latihan untuk mengasah pemahaman Anda tentang fungsi dan relasi. Setiap contoh soal dilengkapi dengan penyelesaian yang detail, sehingga Anda dapat memahami langkah-langkahnya dengan baik. Latihan soal disajikan dalam tabel untuk kemudahan referensi. Soal cerita juga disertakan untuk mengaplikasikan konsep fungsi dan relasi dalam situasi nyata.

Contoh Soal dan Penyelesaian

Berikut beberapa contoh soal untuk memperjelas pemahaman konsep fungsi dan relasi:

Soal: Tentukan apakah relasi (1, 2), (2, 4), (3, 6), (4, 8) merupakan fungsi. Jelaskan alasannya.

Penyelesaian: Relasi tersebut merupakan fungsi karena setiap elemen pada domain (himpunan pertama) berpasangan tepat dengan satu elemen pada kodomain (himpunan kedua). Dalam hal ini, 1 berpasangan dengan 2, 2 berpasangan dengan 4, 3 berpasangan dengan 6, dan 4 berpasangan dengan 8. Tidak ada elemen pada domain yang berpasangan dengan lebih dari satu elemen pada kodomain.
Soal: Diketahui fungsi f( x) = 2 x + 1. Tentukan nilai f(3).

Penyelesaian: Untuk mencari nilai f(3), substitusikan nilai x = 3 ke dalam rumus fungsi f( x). f(3) = 2(3) + 1 = 6 + 1 = 7.
Soal: Sebuah toko menjual baju dengan harga Rp100.000 per potong. Buatlah fungsi yang merepresentasikan total harga ( T) berdasarkan jumlah baju ( n) yang dibeli.

Penyelesaian: Fungsi yang merepresentasikan total harga adalah T( n) = 100.000 n. Misalnya, jika seseorang membeli 3 baju, maka total harganya adalah T(3) = 100.000 x 3 = Rp300.000.

Latihan Soal

Soal

Jawaban

Langkah Penyelesaian

Diketahui relasi (a, 1), (b, 2), (c, 1), (d, 3). Apakah relasi tersebut merupakan fungsi? Jelaskan alasannya.

Bukan fungsi

Ada dua elemen pada domain (a dan c) yang berpasangan dengan elemen yang sama pada kodomain (1).

Jika g(x) = x²

3, tentukan nilai g(4).

Substitusikan x = 4 ke dalam rumus fungsi. g(4) = (4) ² – 3 = 16 – 3 = 13.

Sebuah taksi mengenakan tarif Rp5.000 untuk 1 kilometer pertama dan Rp3.000 untuk setiap kilometer berikutnya. Buatlah fungsi yang merepresentasikan total biaya (C) berdasarkan jarak tempuh ( k) dalam kilometer (dengan asumsi jarak tempuh lebih dari 1 kilometer).

C( k) = 5000 + 3000( k – 1)

Biaya tetap Rp5.000 untuk kilometer pertama. Biaya tambahan Rp3.000 per kilometer berikutnya, sehingga total biaya untuk k kilometer adalah 5000 + 3000( k – 1).

Soal Cerita

Seorang penjual es krim menjual es krim dengan harga Rp5.000 per buah. Buatlah fungsi yang menggambarkan total pendapatan ( P) berdasarkan jumlah es krim yang terjual ( x). Tentukan total pendapatan jika penjual tersebut menjual 20 es krim.

Penutupan Akhir

Apa Itu Relasi Dalam Matematika - Homecare24

Kesimpulannya, materi fungsi dan relasi adalah fondasi penting dalam matematika. Dengan memahami definisi, jenis, operasi, dan grafiknya, serta penerapannya dalam berbagai bidang, kita dapat melihat betapa luas dan mendalamnya konsep ini. Semoga materi ini memberikan wawasan dan pemahaman yang komprehensif tentang fungsi dan relasi.